Category Archives: lessons

D Major Chord

The best way to memorize chords on guitar

Posted on by

In this lesson we will look at a few strategies to use for the best way to memorize chords on guitar. Keep in mind that everybody learns in slightly different ways so if you feel like modifying this method then do so. This method builds on other tips and lessons we have on memorizing chords and it’s worth checking them out as well. One of the most frustrating aspects of learning guitar is memorizing chords so this method should get you off to a flying start.

 

What it takes to memorize guitar chords

Tests have found that it takes at least 20 repetitions of any task for the brain to start the memorization process. This means if you only repeat something 5-10 times it won’t be enough to improve your skills or recall the information later on. Knowing that it takes at least 20 repetitions to start memorizing chords will help us ensure we’re practicing effectively.

Repetition is the key to memorization. If you practice something only once, there’s very little chance you will actually improve your skills and memory. On the other hand, if you repeat the exercise 20-50 times and do the same thing for a few days in a row you will clearly see improvements and increases in skill.

Key Tip #1: When practicing anything, repeat it at least 20 times before moving on

Our five senses are very tightly linked to our memory – think back of the last holiday you had at the beach – can you feel the warm sunlight, smell the salty air and hear the crashing waves? You are more likely to remember in detail an experience if you use more of your senses. Again we can use this when memorizing guitar chords. Instead of simply playing the chords without much thought we need to really ‘experience’ them. Listen carefully to each sound, feel the strings and frets under your fingers, look at the patterns your fingers make on the guitar. If you really pay attention to every detail you will improve your memorization of the chords. Alternatively, if you simply play the chords without much thought involved, there won’t be enough ‘links’ from your senses to help memorization.

Key Tip #2: The more senses you focus on when practicing, the more your brain will remember it

A final tip we can consider when thinking about memory is something called mnemonics. Mnemonics are simply tricks we can use to assist memorization. A detailed lesson on mnemonics for memorizing chords has already been written so check that out for more information.

Key Tip #3: Use mnemonic devices whenever possible to assist memorization

 

The best method to memorize chords on guitar

Now that you understand what it takes to memorize chords, let’s look at a simple step-by-step method to memorize them in the fastest and easiest way possible.

Step 1: Choose four chords to memorize

If you have our flash cards pack, simply pick out four random cards. Choosing chords at random will stop you from choosing what already feels familiar to you and will help you memorize chords you normally wouldn’t try. It also means you can repeat the method over and over and constantly learn new chords.

Step 2: Study the chords

Quite often beginners will skip this step – it’s a big reason why many beginners have so much trouble actually memorizing the chords! So don’t skip it!

The reason why we study each chord is to create ‘links’ to help your brain memorize them. Below is the flash card for D Major. Have a look at all the information on the card for a moment before reading on.

Memorize chords using flash cards

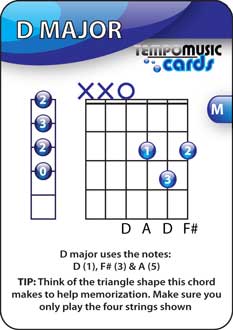
As you can see there’s quite a lot of information on this one chord. Here’s a quick list of points you should think about when looking at this card:

  • The chord uses only four strings – D, G, B, E
  • The notes used are D, F#, A
  • The chord is a Major chord
  • Only the first three fingers are used
  • The finger pattern creates a triangle shape on the fretboard
  • The Guitar TAB layout for the chord (shown on the left of the card) creates a pattern 0 2 3 2
  • The lowest note is the low D string

Can you see how all this information help you memorize the chord? The more you understand the chord before you actually try to play it the easier you will find it to memorize. It’s not enough to simply know where to place your fingers, you need to really understand what is happening for your brain to memorize it faster.

After you spend a minute or two studying each chord you can move on to the next step

Step 3: Visualize playing the chords

Some people may read that and think ‘just play the chord!’, but remember that every time you add in these steps and involve more than one sense you will improve memorization. Visualizing the shapes you form on the fretboard and imagining playing them will actually help you play them! It may feel weird at first to imagine playing the chords, but it really does have an impact on how well you memorize chords.

Simply close your eyes and imagine playing the first chord. Then imagine changing your hand from the first chord to the second and so on until you repeat the four chords twice.

Step 4: Play the progression 20+ times

Now you can pick up the guitar and slowly move from one chord to the next. Notice how you don’t touch the guitar until step 4? That’s why this method is so effective – it makes use of all the available tricks to memorize chords instead of just trying to play them.

At this point it’s important you take your time and really focus on each chord. Remember to think about all your senses while playing as it will assist memorization. Play each chord four times before moving on to the next chord. Repeat the progression at least 20 times.

Step 5: Take a break

It’s important you give your brain time for the chords to sink in. Practicing them too much at the start won’t help you out. Simply taking a break for a couple minutes or having a quick walk is enough to refresh your mind. Don’t be fooled into thinking that an hour of constant practice will help you memorize chords. You’re better off with short and intense practice bursts rather than long and boring practice. If you really concentrate during the first four steps you should feel like you need a break at this point.

Simply take a couple minutes break from the chords to let them sink in.

Step 6: Repeat

Write down the chord progression you just practiced so you can come back to it later on. Plan on practicing the steps for that progression every day for the next week. At this point you can now start again at step 1 and pick out four new chords. Repeat the process with the new chords. Do this a few times until you feel like you can’t concentrate 100% on the task. Once you feel your concentrating fading it’s time to stop and move on to something else. Don’t overdo it as it will actually take you longer to memorize chords.

Why this method works to memorize chords

This method is effective in helping you memorize chords because it requires you to really think about the chords and not just play them. Too many beginners think that if they just play the chords that’s enough to memorize them. When you spend time thinking about the chords and studying them, you will actually find that you can recall the information easier and play them quicker.

Try out this method the next time you want to learn some new chords and you’ll find out just how effective it can be. If you haven’t already got our guitar flash cards pack, consider getting one as it contains 50 basic chords chosen specifically for beginners. It’s a great starting point when used with this method. Follow the advice and steps above and you will memorize chords in less time as well as learning more about each chord.

How to learn guitar chords at home

Posted on by

Learning guitar chords is one of the first things you will learn when starting guitar. If you plan on teaching yourself how to play, there are a few different ways you can learn guitar chords at home. In this article we will look at how you can teach yourself guitar chords at home using a few simple methods. If you have a teacher and are looking at other ways to learn chords, then these methods will help you out too.

Following a method vs just playing chords

Quite often when beginners ask me for help on how to teach themselves to play, they often mention that they just play the chords until it works. This is a problem many self taught guitarists face – they don’t realize there’s better ways to learn. If you’re currently teaching yourself how to play guitar or thinking about teaching yourself, keep in mind that unless you follow a method it’s going to be a long and hard process. ‘Just playing chords until it works’ is a long and frustrating way to learn chords. Learning guitar using this trial and error approach takes a lot longer than following methods that have been proven to work.

When you follow a method you have the piece of mind knowing that it’s worked for other people before you. Instead of guessing what to do you can simply follow the steps given. Following a method allows you to completely focus on what you’re doing instead of thinking the whole time ‘is this going to work?’ Next time you want to learn a new technique on guitar, try to find a method or practice plan that other people have used before. You will save a lot of time doing this and you will learn faster and easier as a result.

What you need to learn guitar chords at home

As explained above you need a method to follow to learn guitar chords on your own. You’re going to learn a lot faster with a method instead of just trying to play songs. The next thing you will need is a wide range of guitar chords to learn. Rather than figure out on your own which guitar chords you should learn, having a set of easy guitar chords picked out for beginners will save you a lot of headaches. Our flash cards pack, 50 Essential Chords, was developed to contain 50 easy guitar chords that any beginner can learn. Using this resource will help you learn guitar chords faster because you will have 50 chords already chosen for you.

The last thing you will need to learn guitar chords is patience. Don’t underestimate how important this one is. If you expect to learn all 50 chords in a couple of days then you’re just going to get frustrated. Learning guitar is always hardest at the very beginning because everything feels impossible. The first time you try to play chords it will seem like your fingers can’t stretch that far and the chords just don’t sound right when you play them. But if you have patience, you will know that in time it will get easier and eventually you will be able to play them. Having patience is the key to becoming a pro at guitar.

How to learn 50 chords in 10 minutes a day

We have put together a method to help beginners learn guitar chords at home in 10 minutes a day. If you set aside 10 minutes every day for some solid practice, you will learn guitar chords faster than you might think. Our method breaks the practice down into simple steps that focus on each chord to help you learn in the most efficient way. Read through the method here and download the pdf. The pdf contains a breakdown of what to practice and you can print it out and stick it up on your wall to help you remember what to practice. We have had great feedback from beginners who used this method and managed to eventually memorize all 50 chords.

A quick checklist

So what do you really need to learn guitar chords at home? Here’s a quick checklist on the essentials.

Notice how short the list is and how simple it sounds. The reason so many beginners get stuck is because they don’t consider what actually works. When you take a trial and error approach and just play the chords it’s going to take a lot longer than focusing on one simple method.

What to do after you learn the chords

Once you do learn some chords on your own, it’s time to start applying them. Here’s a quick list of things you can try after you learn some basic chords:

There are many more different ways you can use chords but if you give these a go you’ll start to enjoy using chords and your playing will start to improve at a faster pace. Don’t underestimate the value in these simple steps – there isn’t any secret shortcut – simply follow the steps in the method and you’ll learn the chords in no time at all.

7 Things You Can Do Today to Change Your Guitar Playing Forever

Posted on by

Most of the things you do when practicing or learning guitar will give your playing skills and knowledge a slight boost. Over time these slight boosts help you develop as a player. On the other hand there are things you can do that will dramatically change the way you play guitar forever. That’s a pretty bold statement but once you give these 7 actions a go you’ll see the big improvement in your playing.

 

Action 1: Play something you have never played before

I don’t mean a new song or learn a new solo, but to play something completely new. This is actually a lot harder then you may think. Just pick up your guitar now and spend twenty seconds improvising. Now think about what you just played. What position did you play in? Did you straight away play in a familiar position on the neck? Did you play licks that you normally play when you improvise? How much of what you just played was completely different to what you normally do?

 

The revealing truth is that when most of us improvise, what we normally do is recycle ideas we have heard from other players or ideas we have used ourselves over and over. This happens subconsciously so although we may think that we’re creating something completely fresh – we’re not. If you don’t believe that, try playing something again then analyze what you just played. If you’re honest with yourself you will realize that we do in fact play in a ‘safe zone’ where we reuse the same ideas and principles over and over. When you first pick up your guitar and play something, it’s a pretty good bet that you automatically follow a certain routine and loosely play the same thing every time. This action will help you break that automatic process that doesn’t help you improve.

 

So the challenge in our first action: really try to play something completely different. Throw everything you know about scales, rhythm, melody, phrasing, etc. out the window and try to create something completely different. This is an extremely tough job and it will take a few attempts before you start to break free of your own comfort zones. But once you create something that you truly know is something you have never done before, the ‘aha’ moment you have will open a new door to your playing.

 

What will this do for your playing?

It will help you learn to be truly creative. As crazy as that sounds it’s true.

 

Action 2: Use your guitar to mimic a singer

Choose a song where you love the vocals. Choose a song where you know the vocal parts so well you can hear them in your head without needing to listen to the song. Now take your guitar and try to replicate the vocal parts.

 

To do this you first need to find the right notes. Start off by focusing on a single line. Work out the notes you need to play and play along with the song. Then spend some time thinking about how you need to play each note to get as close to the vocal quality as you can. This is tough so take your time. Listen to the line in the song over and over and really focus on each nuance. Try to copy each nuance using your guitar and really push yourself to open up your playing and match the singer as close as possible.

 

What will this do for your playing?

It’s one thing to play the right notes. To make your guitar sing changes the game completely. When you learn to make your guitar sing as if it were alive, you will never look back. A guitarist like Santana (and countless others) can create a whole song around four notes if he can make those notes sing.

 

Action 3: Give somebody a guitar lesson

You may feel like you fully understand a certain concept or principle until you try to explain it to a beginner. Trying to explain proper vibrato technique to a beginner is quite a challenge and forces you to really think about your own technique habits. Teaching guitar forces you to really make sure you demonstrate everything perfect because you don’t want your student to pick up on any bad habits you may have formed. In other words it’s a great way to put the microscope on your own technique and habits and really make sure you do everything perfect.

It will also test how well you really know concepts such as music theory. How would you explain what C7 means to a beginner? Or how would you explain the Dorian mode? You may think you can explain it properly but what happens if you student doesn’t understand and you need to think up a different way to explain it?

 

To complete this task all you need to do is give anybody a lesson. For sure one of your friends would have mentioned in the past that they would love to play guitar. Well give them a free lesson on the basics. You might be surprised how challenging it can be to properly explain the techniques you do automatically.

 

What will this do for your playing?

Learning to explain tricky techniques and theory to somebody else reinforces your own skills and understanding. Teaching other people to use proper technique will ensure that you follow it too!

 

Action 4: Write an article or lesson and submit it as a guest post on a guitar blog

This may seem like a strange task at first. But writing about a certain aspect of guitar playing opens your mind to think about how you play guitar in new ways. Imagine for a moment you had to write an article about your practice habits, what would you write? Do you practice in an effective way or can you think of better ways to practice? As soon as you put down the guitar and ponder over a topic like this, you start to see outside the box.

 

Here’s a few topics you could write about to get you thinking about your playing in new ways:

  • How to start improvising
  • Learning to transcribe music by ear
  • How to discipline yourself to perfect your techniques
  • Being creative
  • Writing melodies on guitar
There are so many different things you could write about and each time you do so, your level of understanding increases. Pick a topic you feel confident in to start with then after you write up a lesson, try another one on something you’re lesson confident with.
Submit it to any guitar site offering it as a guest post. Ask for feedback on it and for them to let you know if they don’t want to use it. That way if they don’t want to use it (don’t take it personally) you can send it to a different site. Do this to hopefully get some constructive feedback from experienced guitar writers. They may find out that your understanding of the topic isn’t quite right. This challenge is a great way to learn something about your level of knowledge and try to find ways to improve it. If you send your article to a blogger and they like it, you may even decide to write regularly on guitar topics.

 

What will this do for your playing?

This challenge will help you get a clear view of your current level of knowledge. You may feel like you understand a certain aspect of theory properly (eg: modes) but until you write about them, you won’t know for sure. Once you start writing on a topic you will find out how well you truly know the subject. This will all help you improve as a guitarist as it will help you refine your understanding of guitar and the theory involved.

 

Action 5: Spend 30 minutes playing only two notes

When you jam with somebody or just improvise on your own, you probably play all over the neck or at least a fairly large section of the neck. Because you are so used to playing a wide range of choices, a challenge like this will feel incredibly difficult. The aim of this challenge is to get you used to making the most out of a very limited number of notes. By doing this task you can work your creativity and make the most of what you have.

 

To accomplish this challenge, simply play the two notes below in as many different ways you can for 30 minutes.

 

Set a stopwatch or countdown timer for 30 minutes and only play those two notes. You can only play the two notes shown, you can’t play D or E anywhere else on the neck. The two notes you play have to be on the seventh and ninth frets on the G string (as shown). The reason for this is to limit your choices down to actually using the notes rather than thinking about where else you could play.

When you start this challenge, depending on your current skill level you will start to run out of ideas after the two minute mark. If you give up at this point you will completely miss the point. By continuing past this two minute mark you will force yourself to come up with fresh new ways to play these two notes that you haven’t tried before.

The longer you can last without repeating your ideas the more your creativity will grow. The reason this challenge is so difficult is because we are all used to having a wide range of choices and the ability to freely play in different positions and choose different notes. When you are forced to actually think about how you will use the notes instead of thinking about what the next note will be, you start to learn to really play. You probably won’t last 30 minutes but the longer you do last the more you will learn and improve.


What will this do for your playing?

If you can successfully play these two notes for 30 minutes without getting stuck for new ideas, imagine what you can do with three notes. Imagine what you can do with a whole fretboard! After the grueling 30 minutes of struggling to come up with fresh ideas, you will really start to think about making each note count. This effect is obvious when you compare the jamming of an intermediate player versus an expert player. The intermediate play will shred like crazy, filling their playing with lightning fast scale runs. The expert play may play some shred and include scale runs, but they will do so only when it’s suitable, and they will choose very selectively which notes they play. They make each note count.

This challenge will change your playing forever because it will get you stuck out of the rut you didn’t even know you were in. It will teach you to make each note count.

 

Action 6: Transcribe a lick or riff by ear

In the past when a guitarist wanted to learn how to play a song they would either buy a sheet music book, or if they were unavailable as they often were they would learn by ear. This is a skill which is quickly dying off as countless TABs are available in an instant online. It’s a bit of a learning curve to figure something out by ear and when it’s so easy to download a TAB instead, well it’s no wonder people prefer the instant option. This challenge is to get you used to using your ears and learning to hear the music rather than read it.

 

Choose a song where you haven’t seen the TAB before and choose an interesting lick or riff you would like to learn. It’s best to do this at a computer so you can easily playback the lick or riff over and over without having to fiddle around with rewind on a CD player or iPod. Listen to the lick a few times in a row then try to play it on your guitar. Just give it a go and fish for the notes that sound about right. Listen to the lick again a few times and make adjustments to what you played. Continue the pattern of finding the right notes, listening to the lick, then making adjustments. Keep on making adjustments until you’re certain that the notes you are playing are exactly the same as what you’re hearing.

Once you complete this challenge and manage to figure out an entire lick or riff by ear, you can choose to keep going and learn an entire solo, or an entire song. But even if you just learn a single lick or riff by ear, it puts you miles ahead of so many other guitarists.

 

What will this do for your playing?

Very few guitarists starting to learn today will learn this skill. Not because they are lazy, but because TABs are so accessible it never occurs to them that this skill is important. Learning to develop your listening skills is paramount to becoming a great musician. You may already be a great guitarist but with this skill you can become a great musician as well.

 

Action 7: Jam with other musicians

This will have a huge impact on your abilities especially if you have never done it before. If you do regularly jam with other musicians, we can change this action to jam with other musicians playing an instrument you have never jammed with before. So if you have never jammed with somebody playing a Trumpet, try to find somebody who plays it then jam with them.

The reason jamming with other musicians is so powerful is because it helps you gain a new perspective on music. Seeing how another musician improvises and uses your ideas to come up with new variations is a great way to improve your creativity. You will be able to bounce ideas back and forth and try things new you haven’t done before (see action 1).

The more different the musician you jam with is to you the better. If you’re a metal player and jam with another metal player, you may learn a bit but it won’t be anything compared to what you would learn if you jammed with a jazz player or a player who plays something else completely different to metal. The idea here is to break out of your comfort zone and try something new.

 

What will this do for your playing?

Every single musician you jam with will teach you something regardless of their level of expertise. Even a beginner will teach you something (often what not to do). Whenever you have the opportunity to jam with another musician, make sure you take full advantage and go for it. Even if the musician plays a style you don’t like, just keep an open mind and you may still learn something. One of the easiest ways to kill any progress you make as a musician is to have a closed mind. Jamming with other musicians with an open mind could possibly have the biggest effect on your playing out of these seven actions.

 

What next?

You may notice that some of these actions you have done before and some you haven’t. The whole point is to try something completely new to you to grow your comfort zone and learn new skills. So after you try these seven actions, you can keep going by finding new ways to challenge yourself. Whenever you come across a guitar lesson or anything else that you haven’t done before, give it a go. It’s the only way to make real progress as a guitarist. If we keep doing the same things over and over, we might gradually increase our skills and abilities but they won’t dramatically change in new ways. These seven actions will each give your development a massive boost in very different ways.

 

These seven actions were chosen because you can do them again and again and still learn from them. Make it a personal goal to try to play something completely different (action 1) every time you practice. Next time you hear a nice lick or riff that you want to learn, don’t just go find the TAB, try to work it out on your own (action 6). Whenever you meet a musician ask them if you can jam with them some time (action 7). Every time you repeat these actions you will learn new things and become a better guitarist and a better musician.

Found this lesson useful? Share it by clicking the icons below so others can learn too. Check out more lessons here.

New lesson: Learn how to extend basic chords across the fretboard

Posted on by

A new lesson has been added to the Lessons Section that will help you master the fretboard and build up your chord vocabulary. The lesson will explain how to take a basic chord and find new positions across the fretboard. This is a skill not many guitarists know well so take your time to read the lesson and you will be ahead of the game.

Access the lesson here: Extending chords across the fretboard

If you have been wondering how you could improve your improvisation skills or want to be able to come up with new and interesting chord progressions, this lesson will give you a valuable tool to do it.

New lesson: Seven different ways you can play chord progressions

Posted on by

If you’re learning basic chords and how to put together chord progressions, this new lesson will help piece all the different lesson ideas together. How you play chord progressions is often overlooked by guitarists. Many stick to the standard method of strumming which really is the ‘default’ option. This new lesson gives you seven different ways you can play chord progressions which is more than enough to give you fresh ideas for countless songs. The whole idea is to help you learn to find new ways of playing chords and avoid the default (and boring) methods.

Check out the lesson here: Seven different ways you can play chord progressions

The lesson provides examples for each method so you can start applying them straight away. Also included are links to other lessons in case you need to brush up on some technique.

Using flash cards to master guitar chords

Posted on by

INTRODUCTION

There are so many different ways you can learn guitar that most people don’t know about. So many think the old way of learning with a guitar book is the best and only way to learn. It isn’t. Everybody learns differently so learning from a book is very limiting. It doesn’t allow you to learn the way that suits you best. In this article we will look at why flash cards can be so effective and how you can use them to become an expert at basic open chords.

WHY FLASH CARDS WORK

You probably know of flash cards as those basic cards with a word on one side and a picture on the other used for children to learn basic words. Everybody knows they are effective in teaching children the basics but many don’t realize they are effective in other uses. Whether learning a foreign language, preparing for exams or even learning guitar chords, flash cards have been proven to be very effective learning tools.

Flash cards are so effective because you use them differently than you would use a book. People are used to picking up a book and reading it from cover to cover. Once they read it through the first time, it’s unlikely they’ll go back to the start. With flash cards you can use them in so many different ways. You can play memory games, study one at a time, flick through them trying to memorize the details, really whatever you want to do with them. Because of this flexibility, flash cards end up being more effective than a book despite having less information.

HOW TO BECOME AN EXPERT AT CHORDS

Think about what it means to be an expert at chords. An expert can:

  1. Instantly recall chords
  2. Change back and forth between chords effortlessly
  3. Understand everything about the chords.

 

Now that we know what it takes to become an expert at chords we can look at how to get there.

1. Instant recall

If we want to practice the first goal – instant recall, we can take some flash cards and play memory games. This is something a book won’t teach you. Memory games with flash cards are easy and can be fun which makes it even easier to learn. You don’t even need to have a guitar with you to become an expert at the first goal; you can play memory games with flash cards anywhere and anytime.

2. Changing between chords

To become an expert at the second goal – changing back and forth between the chords you simply need to practice every combination of chord changes. With flash cards this is easy. You simply pick out two cards and practice changing between them until it feels easy. Then you simply change one of those cards. You continue changing card combinations and eventually you will feel comfortable playing any chord change. It’s so simple yet so effective.

3. Chord understanding

To become an expert at the third goal – know everything about the chords, you need to understand a bit about music theory and the chord names. This may sound harder, but it doesn’t have to be.

You start off by memorizing the chord names. That’s pretty easy to do. You will probably do that with the memory games mentioned earlier. Once you know the chord names you can start to learn what they mean. What makes a major chord? What does sus2 mean? What’s the difference between E9 and Eadd9? The good thing is that once you know what each type of chord means then your songwriting, playing and understanding of music will improve. Flash cards will give you a starting point to understanding chords as you can look at the notes that make up the chords and see the patterns between the cards.

RESOURCES

This site has a few different resources to help you achieve the three goals described above. Think which goal would help you out the most then check out the related resources to get started.

Flash Cards – Available here

Instant recall resources:

Changing between chords resources:

Understanding chords resources:

 

SUMMARY

You should be able to see that everything written above is fairly simple to do. There’s no magic formula or secret to becoming an expert, it’s simply practice with the right tools. Practicing with flash cards is a great way to speed up the learning process. You can become an expert at chords with a book, it just takes longer and can be a bit harder to stay motivated. Once you become an expert at chords, you will be amazed at how many doors open up in your playing and songwriting. It’s definitely worth the effort. The resources listed above will walk you through step-by-step and break down all the concepts with simple explanations and examples. You can read more on the flash cards pack available on this site here.

Guitar Chord Exercise 1

New guitar lesson: Finger exercises to help you play chords

Posted on by

If you are starting to learn guitar chords, this new lesson will help you loosen up your fingers and stretch them out which will make the chords a lot easier to learn.

This lesson – Simple exercises for beginners: Stretch Part Two – will give you two very simple exercises you can use as a warm up whenever you try to learn some new chords. You can also check out Stretch Part One for some similar exercises that will get you used to using the correct hand position as well as stretch your fingers out.

Give the exercises a good workout but remember to stop if you feel any pain and come back to the exercises later on.

Lesson at ultimate-guitar.com How to come up with your own exercises

Posted on by

This lesson over at ultimate-guitar.com explains why it is important that you learn to come up with your exercises to help you learn techniques or improve your skills. There will be a time when you can’t find any relevant exercises for a technique you want to develop. This lesson spells out step by step what you need to do to come up with effective exercises.

An analysis of an exercise is included to show you how you can do the same and what really makes an exercise effective.

Access the lesson here.

Although all guitarists should learn how to come up with effective exercises, this lesson is suited for intermediate to advanced players.

How to write your own Guitar TAB for your song ideas and riffs

Posted on by

Being able to read Guitar TAB is obviously a crucial skill to every guitarist. But some people don’t consider how important it is to learn to write TAB as well. Learning to write your own TAB is very simple and will help you out in a few different ways.

Writing your own TAB can help you:

  • Write down any song ideas
  • Ensure you don’t forget any riff or lick ideas you come up with
  • Transcribe songs
  • Write full songs to give to other players to learn
  • Come up with a collection of your own riffs and licks

This lesson here will explain the basics and the points you need to remember when trying to write your own TAB. The lesson is very straight forward because if you can already read TAB then you’re half way there.

You can access the lesson here – Learn to write your own Guitar TAB

Included in the lesson is a free Blank Guitar TAB Sheet you can download, print out and use straight away for any ideas you come up with.

New Guitar Lesson: Create your own rhythm and strumming patterns

Posted on by

This new guitar lesson will explain the basics of rhythm and how you can come up with your own rhythm patterns. The lesson will explain standard notation as well as provide you with a blank rhythm sheet you can print out for your own ideas.

This is a very basic exercise worth learning. Learning to write out rhythm patterns can help you:

  1. Write strumming patterns for chord progressions
  2. Transcribe strumming patterns from songs by ear
  3. Learn to play along with a drummer
  4. Give drummers ideas for beats and patterns
  5. Add an interesting rhythm to your licks and melodies
  6. Write riffs that are focused on a rhythm pattern

 

You can access the lesson here:

Create you own rhythm and strumming patterns

There are many more things you can do when you develop this skill so check the lesson out and start coming up with your own ideas.